2016年麻布中学の問題です。
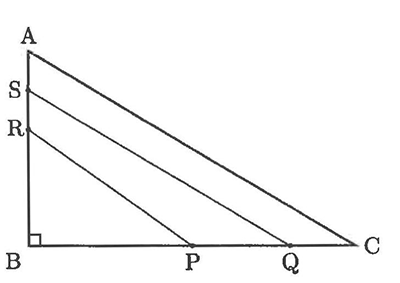
図のように、角Bが直角である直角三角形ABC、直線PR、直線QSがあります。
BP:PQ:QC=3:2:1であり、2つの直線PRと直線QSによって三角形ABCの面積が3等分されています。
このとき、BR:RS:SAを、最も簡単な整数の比で答えなさい。
みんな同じ面積ですから、三角形ABCの3分の1です。
三角形BRPは3分の1だから、
$$\frac{1}{2}$$×$$\frac{BR}{AB}$$=$$\frac{1}{3}$$ より$$\frac{BR}{AB}$$=$$\frac{2}{3}$$
三角形SBQは三角形ABCの3分の2になるので、
$$\frac{5}{6}$$×$$\frac{BS}{AB}$$=$$\frac{2}{3}$$ より$$\frac{BS}{AB}$$=$$\frac{4}{5}$$
AB=15とすると、BR=10 BS=12よりBR:RS:SA=10:2:3
(答え)10:2:3
==============================================================
受験で子どもと普通に幸せになる方法、本日の記事は
2016年中学受験
==============================================================
今日の慶應義塾進学情報
マナーに関する問題
==============================================================

==============================================================

==============================================================

==============================================================
![]()
にほんブログ村

