2014年 暁星中学の問題です。
ある中学校の1年生全員の住所と血液型を調べました。X市に住んでいる生徒は112人いました。Y市とZ市に住んでいる人数の比は7:3で、X、Y、Z市以外に住んでいる生徒はいませんでした。また、A型とB型の人数の比が7:5で、AB型の人数はZ市に住んでいる人数の半分でした。そして、O型の生徒は1年生全員の4分の1で、B型とAB型の生徒の合計は67人でした。このとき、次の各問いに答えなさい。ただし、血液型はA、B、AB、Oの4種類しかいないものとします。
(1)次の空らんを埋めなさい。ただし、( ア )は分数で、( イ )には整数が入ります。
「A型とB型の人数の差はY市とZ市に住んでいる生徒の合計の( ア )に( イ )人を足したものである。」
(2)1年生全員の人数を求めなさい。
(1)
条件を整理するために表にしてみましょう。
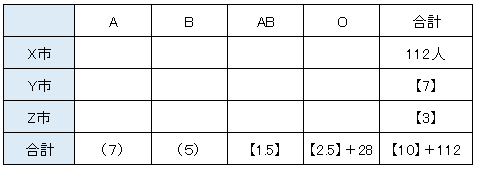
Y市とZ市に住んでいる人の比が7:3ですので、これは【7】、【3】とします。X市に住んでいる人は112人ですから、全体は【10】+112人になります。
AB型の人はZ市に住んでいる人の半分なので【1.5】となり、O型の生徒は全体の$$\frac{1}{4}$$になるので【2.5】+28人と表すことができます。
すると全体の人数は(12)+【4】+28=【10】+112
(12)=【6】+84人
6で割れるので
(2)=【1】+14人
ここで(2)はA型とB型の人数の差になります。それが【1】+14人で【1】はY市とZ市に住んでいる人の数の$$\frac{1}{10}$$ですから、アが$$\frac{1}{10}$$、イが14です。
(答え)ア $$\frac{1}{10}$$ イ 14人
(2)
B型とAB型の人数の合計は67人です。したがって(5)+【1.5】=67人
(2)=【1】+14人から(5)=【2.5】+35人
したがって【2.5】+【1.5】+35人=【4】+35人=67人 【4】=32人 【1】=8人
1年生全員の数は8×10+112=192人です。
(答え)192人
6年算数頻出問題精選ノート(田中貴)
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
部活のウェイトは大きい
==============================================================
中学受験 算数オンライン塾
9月30日の問題
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村

