2014年聖光学院の問題です。
身長100cmのひかる君は正方形の鏡を使って、実験1~実験3をおこないました。あとの(1)~(5)の問いに答えなさい。ただし、ひかる君の目の高さは床から90cmです。また、鏡の厚さは考えないものとします。
[実験1]図1のように、ひかる君は、ある大きさの正方形の鏡を壁に取り付けました。壁から100cmの場所に立ったところ、頭の先と足の先がちょうど鏡の上下の端に映りました。
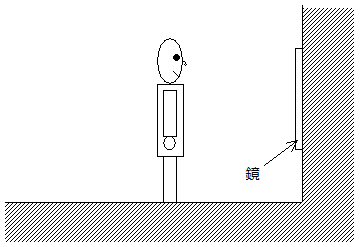 図1
図1
(1)鏡の1辺の長さは何cmですか。
(2)鏡の中心の高さは、床から何cmですか。
[実験2]図2のように、1辺の長さが50cmの正方形の鏡を、その中心が床から90cmの高さになるように、壁に取り付けました。そして、ひかる君は壁から100cmの場所に、身長180cmのお父さんは壁から200cmの場所に立ちました。ひかる君が鏡をのぞいたら、鏡を通してお父さんの体の一部が見えました。
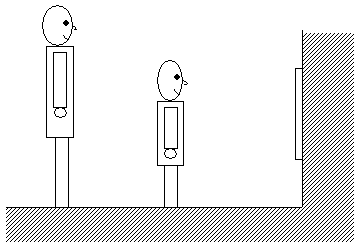 図2
図2
(3)鏡に映ったのは、お父さんの体のどこからどこまでですか。その範囲を、床からの高さで答えなさい。
(4)お父さんだけが撃から少しずつ離れていきました。お父さんがある場所まで移動したとき、ひかる君は鏡を通してお父さんの全身を見るととができました。お父さんの全身が初めて見えたとき、お父さんは壁から何cm離れていましたか。
[実験3]1辺の長さが40cmの正方形の鏡を、その中心が床から90cmの高さになるように、壁に取り付けました。図3はその様子を真上から見たものです。そして、身長180cm、肩幅60cmのお父さんは、壁から120cm、鏡の端から130cmずれた場所に立ちました。ある場所に立ったひかる君か鏡をのぞいたら、鏡を通してお父さんの体の右半分だけが見えました。次に、ひかる君が壁に対して平行に、右へ32cmだけ移動したところで、お父さんの全身が初めて見えました。
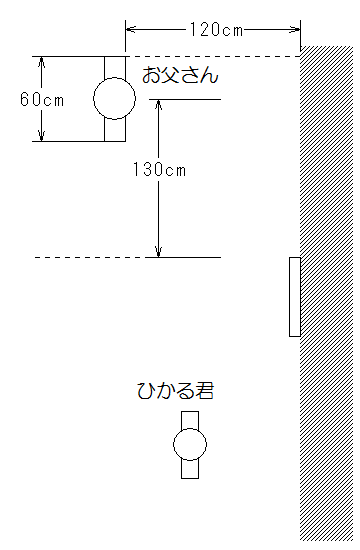 図3
図3
(5) ひかる君は右へ移動しなくても、壁に対して垂直に近づけば、鏡を通してお父さんの全身を見ることができます。このようにしたとき、お父さんの全身が初めて見えるのは、ひかる君が壁に何cm近づいたときですか。
(解説と解答)
(1)下図4のように、鏡の向こうの像は鏡から100cmのところにあります。
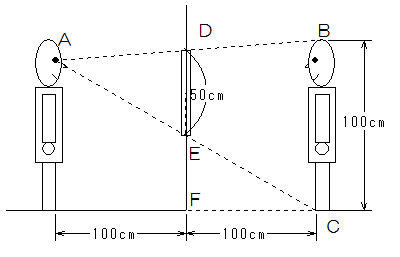 図4
図4
ここでひかる君は自分の全身を見ることができたので、鏡の高さは図のDEの長さになります。
三角形ADEと三角形ABCは1:2の相似の三角形ですから、DEの長さは50㎝になります。
(答え)50cm
(2)図4でAは下から90cmですから、EFの長さは90÷2=45cmなので、鏡の中心は45+50÷2=70cmのところにあります。
(答え)70cm
(3)鏡の高さは50cm、中心が下から90cmですから、90-50÷2=65cmが鏡の下辺になります。
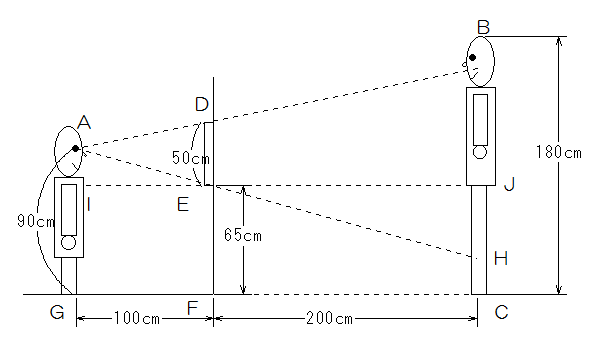 図5
図5
お父さんの像が鏡の反対側の200cmのところにあり、お父さんの身長は180cmです。したがってGF:FC=1:2よりお父さんの像は鏡には、50×3=150cm分しか映りません。
ひかる君の目の高さが90cmですから、鏡の下辺との高さの差(AI)は
90-65=25㎝ したがってHJの高さは25×2=50cmなので、HCは65-50=15cmになります。
お父さんは下が15cmから上が15+150=165cmまでしか見えません。
(答え)15cmから165cmまで
(4)鏡の高さが50㎝しかありませんので、図のGF:FC=50:180-50=5:13になれば、お父さんの像は全部見えることになります。
ひかる君の位置は変わりませんから、100÷5×13=260cmお父さんは壁から離れれば良いことになります。
(答え)260cm
(5)お父さんの肩幅は60cmですから、半分は30cmです。
ひかる君は32cm動くことで30cm、視野が広がったので、
ひかる君からかべまでの距離:かべからお父さんまでの距離=32:30=16:15
お父さんから壁までの距離が120cmですから、ひかる君は120÷15×16=128cm、かべと離れています。
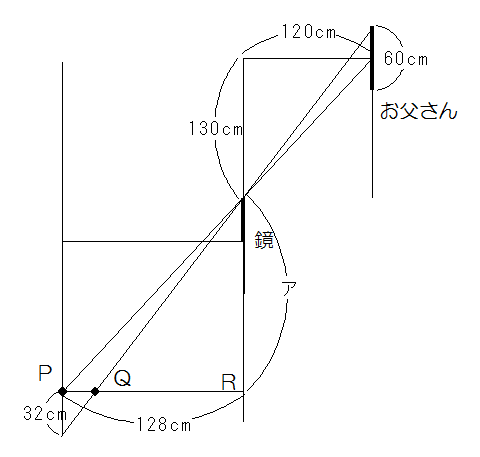 図6
図6
ひかる君はQに出てくれば、お父さんのすがたを全部見ることができます。
図6でアの長さは130÷120×128=$$\frac{416}{3}$$
PQ:QR=32:$$\frac{416}{3}$$=3:13
したがってPQの距離は128÷(13+3)×3=24cmになります。
(答え)24㎝
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
やり方を覚える、のワナ
==============================================================
中学受験 算数オンライン塾
8月9日の問題
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村
