2016年渋谷学園渋谷の問題です。
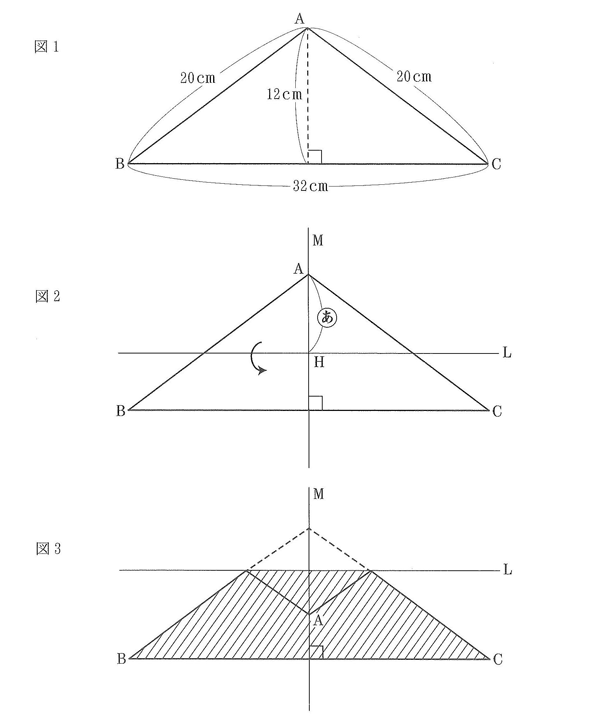
図1のような三角形ABCがあります。図2のように、三角形ABCを辺BCに平行な直線L
について、点Aが直線Mに重なるように折り曲げてできた図形をPとします。例えばAH(あ)の長さが4cmのとき、図形Pは図3の斜線部分です。
次の問いに答えなさい。ただし、円周率は3.14とし、また、すい体の体積は、(底面積)×(高さ)÷3で求めることができます。
(1)図3の図形Pの面積は図1の三角形ABCの面積の何倍ですか。
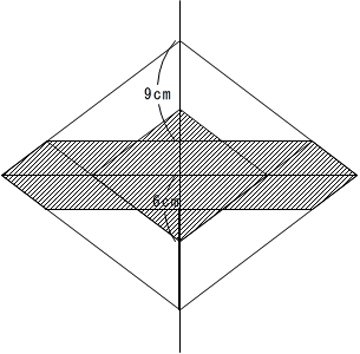
(2)(あ)の長さが9cmのとき、図形Pの面積は何cm2ですか。
(3)(あ)の長さが9cmのとき、図形Pを直線BCの周りに1回転させてできる立体の体積は何cm3ですか。
【解説と解答】
(1)高さが3分の1になるので、面積は9分の1だけ折り曲がったことになります。したがって面積は9分の8です。
(答え)$$\frac{8}{9}$$
(2)9cmになると下にはみ出します。LがBCから3cmのところにくるので、下にはみ出した高さは6cmです。
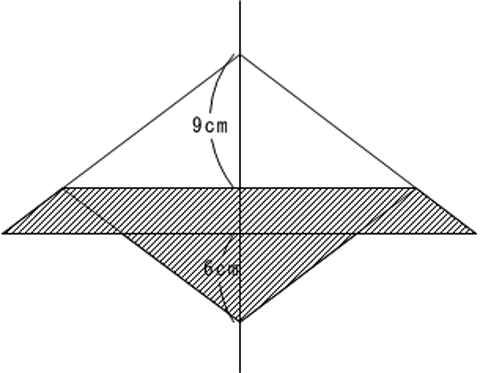
上の部分は4分の3がなくなっているので$$\frac{7}{16}$$ 下にはみ出したのは2分の1なので面積はで$$\frac{1}{4}$$ 合計$$\frac{11}{16}$$なので
32×12÷2×$$\frac{11}{16}$$=132
(答え)132cm2
半径が3cm、高さが4cmの円錐、半径が3cm、高さが8cmの円柱、半径が6cm、高さが8cmの円錐から半径が3cm、高さが4cmの円錐を引いた円錐台。この合計の2つ分になります。したがって、
3×3×3.14×4÷3×2+3×3×3.14×8×2+6×6×3.14×8÷3×(1-$$\frac{1}{8}$$)×2=(24+144+168)×3.14=1055.04cm3
(答え)1055.04cm3
「映像教材、これでわかる比と図形」(田中貴)
============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
忘れたらまた覚え直せばいい
============================================================
中学受験 算数オンライン塾
7月13日の問題
==============================================================

==============================================================

==============================================================

==============================================================
![]()
にほんブログ村