2015年駒場東邦の問題です。
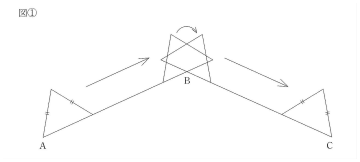
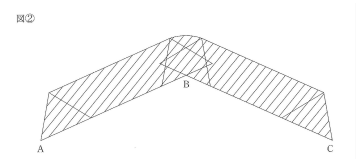
図1のような折れ線ABCにおいて、二等辺三角形をすべらせます。ただし、頂点Bのところでは、折れ線と接している二等辺三角形の辺のまん中の点が頂点Bに来たときに、辺のまん中の点を中心として時計回りに折れ線と辺が接するまで回転し、またすべります。このとき、二等辺三角形が通過したあとにできる図形(斜線部分)が図2です。
必要があれば、円周率は3.14として計算しなさい。
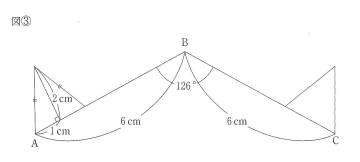
(1)図3のような条件で二等辺三角形が動いたとき、二等辺三角形の通過したあとにできる図形の面積を求めなさい。
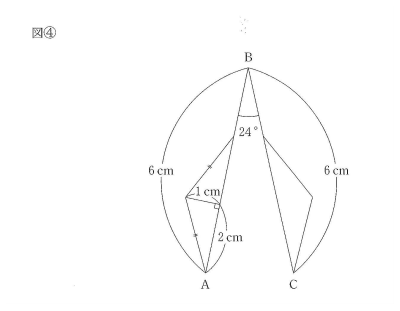
(2)図4のような条件で二等辺三角形が動いたとき、二等辺三角形の通過したあとにできる図形のまわりにおいて、円周の一部となるところの長さを求めなさい。
(1)
回転する部分は半径が2cm、角度が360-90×2-126=54°のおうぎ形の面積になり、それ以外は高さが2cm、横5cmの長方形が2つ、それと二等辺三角形になるので、
2×2×3.14×$$\frac{54}{360}$$+2×5×2+2×2÷2=1.884+20+2=23.884
(答え)23.884cm2
(2)
図のように動きます。
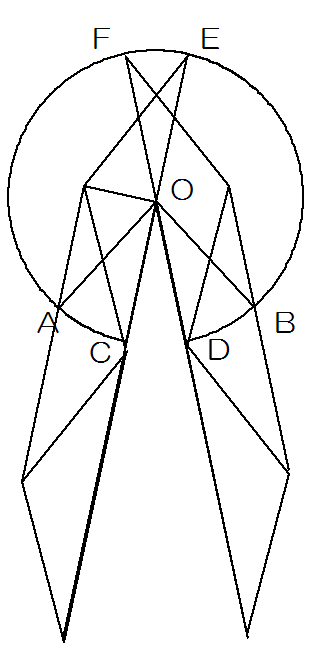
ここで弧EFの部分は通りません。
角CODは問題文の条件から24°ですから、角EOFの角度も24°になります。
また角AOCはOAが2cm、AからOCに降ろした垂線の長さが1cm(二等辺三角形の高さ)ですから、30°とわかります。
したがって弧の中心角は合計360-30×2-24×2=252°
弧の長さは2×2×3.14×$$\frac{252}{360}$$=12.56×0.7=8.792cm
(答え)8.792cm
==========================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
外出する機会を減らす
=============================================================
中学受験 算数オンライン塾
12月22日の問題
==============================================================

==============================================================

==============================================================

==============================================================
![]()
にほんブログ村

