2017年筑波大駒場の問題です。
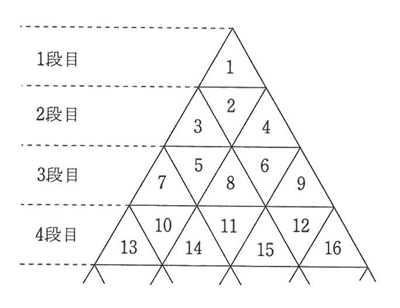
図のように,同じ大きさの正三角形をしきつめて,それぞれの三角形に規則的に1,2,3,4,…と数を書きこみます。
例えば,5は3段目の左から2番目の三角形に書かれています。また,4段目の左から5番目の三角形に書かれている数は15です。
次の問いに答えなさい。
(1)10段目の一番左にある三角形に書かれている数を答えなさい。
(2)2017が書かれている三角形は、何段目の左から何番目の三角形ですか。
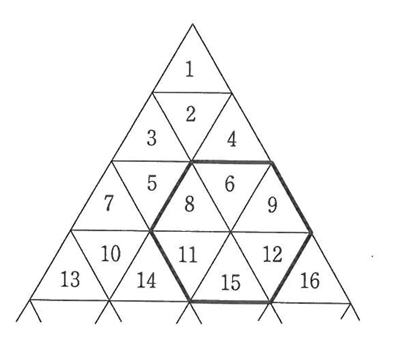
(3)しきつめられた図形の一部で,6個の正三角形からなる正六角形に注目し,その中の6つの数のうち最も大きい数と,6つの数 の和を考えます。
例えば,右図の太線で囲まれた正六角形において,6つの数のうち最も大きい数は15であり,6つの数の和は61です。
6つの数の和が610であるとき,6つの数の中で最も大きい数を答えなさい。
【解説と解答】
(1)n段目の一番右側の数はn×nになっていて、△の段にはn個の数字が並んでいるので、
10×10=100 100-10+1=91
(答え)91
(2)2017に一番近い平方数を考えると、44×44=1936 45×45=2025ですから、45段目の右端から戻ります。
(段、左はしからの列)と表すと、
(45、89)=2025、(45、88)=2025-45=1980
(45、87)=2024、(45、86)=2025-45=1979
(45、85)=2023、(45、84)=2025-45=1978
(45、83)=2022、(45、82)=2025-45=1977・・・ となるので、2025-2017=8から、2×8=16より、
(45、73)=2017
(答え)45段目 左から73番目
(3)右2つの和と真ん中2つの和が同じで、左2つの和はそれより2小さいから、
(610+2)÷3=204
一番小さい数をm、上の段数をnとすると、6つの数字は
m+n-1、m、m+n
m+2×n-1、m+3×n、m+2×n
という関係にあるので、2×m+3×n=204
ですから、(m、n)=(99、2)(97、4)(95、6)(99、8)(87、10)(85、12)・・・となります。
で、mはn段の数ですからn×nよりは小さくなければならず、(n-1)×(n-1)よりは大きくなければなりません。
したがって(87、10)があてはまります。
よって最大の数は87+10×3=117
(答え)117
受験で子どもと普通に幸せになる方法、本日の記事は
あきらめてはいけない
6年生の教室から
楽しく勉強する
中学受験 算数オンライン塾
6月14日の問題