2016年東邦大東邦の問題です。
図のような.大きさの等しい正三角形を八つ合わせてできる立体ABCDEFがあります。BDの長さは4cmです。頂点Bに、この立体の1辺と等しい長さのひもの先端をつけました。 このとき、次の問いに答えなさい。
(1)この立体の体積を求めなさい。
(2)この立体の表面上で、ひものもう一方の先端Pが届く範囲の面積を求めなさい。
ただし、円周率は3.14とし、答えは小数第3位を四捨五入して小数第2位まで求めなさい。

【解説と解答】
(1)図のように、四角形ABFDは正方形になります。
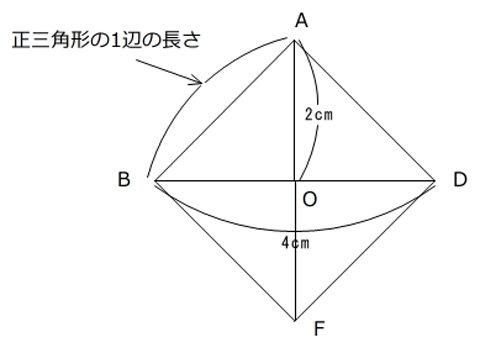
したがってBDとCEの交点をOとすると、OA=2cm。また四角形BCEDも正方形になるので、その面積は4×4÷2=8cm2ですから、この立体の体積は8×2×2×$$\frac{1}{3}$$=10$$\frac{2}{3}$$
(答え)10$$\frac{2}{3}$$cm3
(2)
動く範囲は正三角形の1辺を半径とした中心角60°×4のおうぎ形になります。
正三角形の1辺の長さはわかりませんが、1辺の長さ×1辺の長さ=4×4÷2=8
したがって8×3.14×$$\frac{1}{6}$$×4=$$\frac{10048}{600}$$≒16.746…
から16.75cm2
(答え)16.75cm2
============================================================
受験で子どもと普通に幸せになる方法、本日の記事は
しつこく考える
==============================================================
今日の慶應義塾進学情報
制服
==============================================================

==============================================================

==============================================================

==============================================================
![]()
にほんブログ村

