2015年立教女学院の問題です。
次の( ア )〜 ( エ )にあてはまる数を答えなさい。
Aさんは午後1時何分かに勉強を始めて、午後4時に終わる予定でしたが、気がついた時には午後4時を少し過ぎており、時計の長針と短針の位置が勉強を始めた時と、入れ替わっていることに気がつきました。
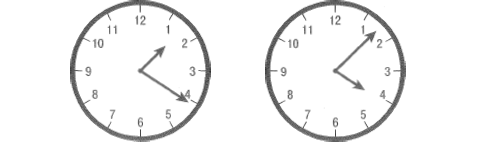
そこでAさんは次のように考えました。
「1分間で時計の長針は( ア )度、短針は( イ )度だけ動く。図から、長針が動いた角度と短針が動いた角度の和は( ウ )度なので、勉強していた時間は( エ )分だ。」
【解説と解答】
短針が動いたのは左の短針の位置から右の短針の位置までです。
長針が動いたのは、左の図の位置から12まで動き、その後、3時、4時と2周してその後右図の長針の位置まで来ています。
したがって、合わせると360×3=1080°であることがわかります。
長針は360÷60=6° 短針は30÷60=0.5°で合計6.5°ですから、1080÷6.5=2160÷13=166$$\frac{2}{13}$$分になります。
(答え)ア 6 イ 0.5 ウ 1080 エ 166$$\frac{2}{13}$$分
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
情緒不安定との戦い
==============================================================
今日の慶應義塾進学情報
カカア天下の空気を読む
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村

