2015年灘中学2日目の問題です。
6枚のカード0、1、2、3、4、5が入った袋が6個あり、袋ア、袋イ、袋ウ、袋エ、袋オ、袋カと名前がついています。これらの袋のうちいくつかからカードを1枚ずつ取り出します。ただし、例えば袋アから2を、袋イから5を取り出した掛合と、袋アから5を、袋イから2を取り出した場合とで、取り出し方は異なるものとします。また、0は5で割り切れます。
(1)袋アと袋イからカードを1枚ずつ取り出すとき、取り出したカードに書かれている数の合計をAとします。次のようなカードの取り出し方は、全部で何通りですか。
(あ)Aが5で割り切れる
(い)Aを5で割った余りが1である
(2)袋ア、袋イ、袋ウ、袋エからカードを1枚ずつ取り出すとき、取り出したカードに書かれている数の合計が5で割り切れるようなカードの取り出し方は、全部で何通りですか。
(3)6個の袋すべてからカードを1枚ずつ取り出すとき、取り出したカードに書かれている数の合計が5で割り切れるようなカードの取り出し方は、全部で何通りですか。
【解説と解答】
(1)
(あ)アに入っている数は0~5、イに入っている数も0~5です。
合計は0~10ですが、5で割り切れる数は0、5、10です。
(ア、イ)=(0、0)(0、5)(1、4)(2、3)(3、2)(4、1)(5、0)(5、5)と8通りあります。
(答え)8通り
(い)1余る数は1、6です。
1 -> (0、1)(1、0)
6 -> (1、5)(2、4 )(3、3)(4、2)(5、1)
(答え)7通り
(2)(1)で2枚のときは8通りでした。
1枚の出方は6通りありますが、これに5の倍数になる数を加えることができるので、6通りと、(0、0)(5、5)で8通りになりました。
では3枚のときに2枚の目の和に、何かを加えればまた5の倍数になりえます。例えば(2、4)と出れば、4を加えればいいことになります。したがって0~5まで6通りの出し方で2枚ですから6×6=36通りに何かを足せば5の倍数になるから、まず36通りあるわけです。
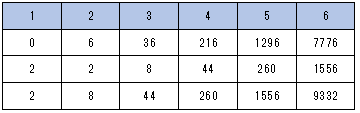
で、それを表にまとめてみました。

このとき和がちょうど5の倍数になるとき、0か5を足すことができます。この数は1枚目の時、ちょうど5の倍数になる数と同じであることがわかります。
したがって3枚目のときは6×6+8=44通りと出すことができます。
同様に4枚目は3枚の値が6×6×6=216通りあるわけですが、これに何かを足せばちょうど5の倍数になり得るので、216通り。また0と5を足せるものが44通りあるので、216+44=260通りになります。
(答え)260通り
(3)(2)から5枚の時は6×6×6×6=1296に260を加えるので1556通りになります。
6枚の時は6×6×6×6×6=7776通りに1556通りを加えるので、9332通りになります。
(答え)9332通り
==========================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
ミス率
==============================================================
今日の慶應義塾進学情報
過去問の記録はほめるために使う
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村

