2015年早稲田中学の問題です。
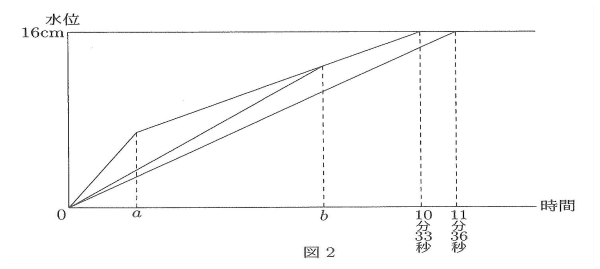
図1のような3辺の長さが20cm、32cm、16cmである直方体の容器の中に、直方体の形をした石Pを入れて、毎分800cm3の割合で水を入れていきました。石の置き方は3通り(斜めに置くことはできません)ありますが、2通りは10分33秒で水があふれ出し、残りの1通りは11分36秒で水があふれ出しました。図2は3通りの石の置き方についての時間と水位の関係を1つのグラフに表したものです。次の問いに答えなさい。
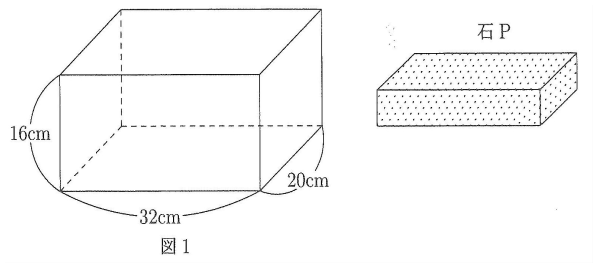
(1) 石Pの体積は何cm3ですか。
(2) 石Pの最も長い辺の長さは何cmですか。
(3) グラフのaとbの差は5分36秒です。石Pの最も短い辺の長さは何cmですか。
【解説と解答】
(1)石Pをたてに置いた時、石が容器の高さの上に突き抜ければ、容器の中の体積は減りますから、逆に水が入る容積は増え、あふれ出すまでの時間がかかります。
したがって、石がすべて入ったときは、水が800×10$$\frac{33}{60}$$=800×$$\frac{211}{20}$$=8440cm3 入るので、容器の容積は16×32×20=10240cm3ですから、その差が石の体積になります。
10240-8440=1800cm3です。
(答え)1800cm3
(2)石が容器の高さを超えて入っていた時は、水の容積が800×11$$\frac{36}{60}$$=800×$$\frac{232}{20}$$=9280cm3入るので、入っていた石の体積は10240-9280=960cm3
したがって960÷1800=$$\frac{8}{15}$$が入っていることになり、それが16cmですから、16÷8×15=30cmが一番長い辺になります。
(答え)30cm
(3)グラフのaは1番短い辺をたてに置いた時、その高さまでくる時間。グラフのbは2番目に短い辺をたてに置いた時、その高さまでくる時間です。その差が5分36秒でした。この時間に800×5$$\frac{36}{60}$$=4480cm3の差があります。石はaのときも、bのときもすべて水につかっていますから、(32×20×2番目に短い辺の長さ-1800)ー(30×20×1番短い辺の長さ-1800)=4480
4480÷(32×20)=7cmですから、2番目に短い辺と1番短い辺の長さの差が7cmです。
1800÷30=60cm2が、その積ですから、12cmと5cmがあてはまるので、一番短い辺は5cmになります。
(答え)5cm
==========================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
同じ問題は出ない
==============================================================
今日の慶應義塾進学情報
慶應湘南2016年度募集要項抜粋
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村

