2015年開成中学の問題です。
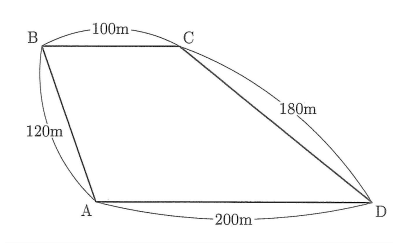
下図のようなランニングコースがあります。A地点とD地点の間の道は平らで長さは200m、B地点とC地点の間の道も平らで長さは100m、A地点からB地点へ向かう道は上り坂で長さは120m、D地点からC地点へ向かう道も上り坂で長さは180mです。
ゆう君はA地点を、まさひろ君はD地点を同時に出発して、ゆう君はA→B→C→D→A→B→・・・の向きに、まさひろ君はD→C→B→A→D→C→・・・の向きに走ります。二人とも平らな道を毎分100mの速さで走ります。ゆう君はA地点からB地点までの上り坂を毎分84mで、C地点からD地点までの下り坂を毎分105mで走り、まさひろ君はD地点からC地点までの上り坂を毎分90mで、B地点からA地点までの下り坂を毎分126mで走ります。
次の問いに答えなさい。
(1)ゆう君、まさひろ君がこのコースを一周するのにかかる時間はそれぞれ何分ですか。
(2)ゆう君、まさひろ君はB地点とC地点の間ではじめてすれ違います。その地点はB地点から何mの場所ですか。
(3)ゆう君、まさひろ君がB地点とC地点の問で次にすれ違うのは、(2)で求めた場所からどちらへ何mずれた場所ですか。
(4)ゆう君、まさひろ君がはじめてÅ地点とB地点の間ですれ違うのは、走りはじめてから何回目にすれ違うときですか。またその地点はB地点から何mの場所ですか。
【解説と解答】
(1)ゆう君はABが上りなので120÷84=$$\frac{10}{7}$$ CDの下りは180÷105=$$\frac{12}{7}$$ 合計$$\frac{22}{7}$$
(200+100)÷100=3分だから1周は6 $$\frac{1}{7}$$分。
まさひろ君はABが下りなので120÷126=$$\frac{20}{21}$$ CDが上りなので180÷90=2分 合計2 $$\frac{20}{21}$$。
それに3分を加えるので1周5 $$\frac{20}{21}$$分
(答え)ゆう君 6 $$\frac{1}{7}$$分 まさひろ君 5 $$\frac{20}{21}$$分
(2)ゆう君がBに来るのは$$\frac{10}{7}$$ まさひろ君がCにくるのは2分後。したがって2分後にはゆう君は
2-$$\frac{10}{7}$$=$$\frac{4}{7}$$分進んでいるので、Bから100×$$\frac{4}{7}$$=$$\frac{400}{7}$$mのところにいます。
二人の間の距離は 100-$$\frac{400}{7}$$=$$\frac{300}{7}$$ mになっているから、その半分のところで出会うので
$$\frac{400}{7}$$+$$\frac{150}{7}$$=$$\frac{550}{7}$$=78 $$\frac{4}{7}$$mのところです。
(答え)78 $$\frac{4}{7}$$m
(3)まさひろ君は1周に5 $$\frac{20}{21}$$分かかるので、次にCにくるのは、$$\frac{20}{21}$$+2=7 $$\frac{20}{21}$$分
ゆう君が次にBにくるのは 6 $$\frac{1}{7}$$分+$$\frac{10}{7}$$=7 $$\frac{4}{7}$$なので、まさひろ君がCを出発するとき、ゆう君はすでに$$\frac{8}{21}$$分進んでいます。
100-100×$$\frac{8}{21}$$=$$\frac{1300}{21}$$ したがって、その場所はBから
$$\frac{800}{21}$$+$$\frac{650}{21}$$=$$\frac{1450}{21}$$=69 $$\frac{1}{21}$$mのところになるので
78 $$\frac{4}{7}$$ - 69 $$\frac{1}{21}$$=9 $$\frac{11}{21}$$
(答え)Bへ=9 $$\frac{11}{21}$$mずれたところ
(4)1周につき9 $$\frac{11}{21}$$=$$\frac{200}{21}$$mずれるので
78 $$\frac{4}{7}$$÷$$\frac{200}{21}$$=$$\frac{550}{7}$$÷$$\frac{200}{21}$$=$$\frac{33}{4}$$
8回ずれるということはBC間で9回出会うことになります。
9周した後、まさひろ君がBにいるのは5 $$\frac{20}{21}$$分×9+2分+1分=56 $$\frac{4}{7}$$分
56 $$\frac{4}{7}$$÷6 $$\frac{1}{7}$$=$$\frac{396}{7}$$÷$$\frac{43}{7}$$=9・・・$$\frac{9}{7}$$
したがってゆう君はAから$$\frac{9}{7}$$分移動しているので84×$$\frac{9}{7}$$=108m 120-108=12mが二人の間の距離です。
ここでまさひろ君とゆう君の速さの比は126:84
12×(126+84)×126=7.2m
二人は1周すると2回出会うので、2×9+1=19回目になります。
(答え)7.2m 19回
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
家庭任せの塾?
==============================================================
中学受験 算数オンライン塾
4月28日の問題
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村

