2014年桐朋中学の問題です。
図のように、辺ADと辺BCが平行な台形ABCDがあります。Eは辺BC上の点で、ABとDEは平行です。この台形をAC、DE、BFで5つの三角形ア、イ、ウ、エ、オに分けるとアの面積は32cm2で、イの面積はエの面積より8cm2大きくなります。
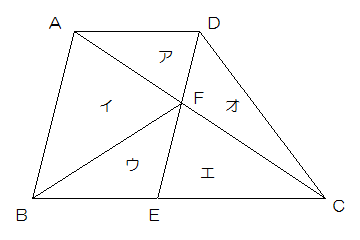
(1)ア、イ、ウ、エ、オのうち、面積の等しい三角形はどれとどれですか。
(2)台形ABCDの高さが16cm、面積が280cm2のとき、ECの長さは何cmですか。
(解説と解答)
(1)
ADとECの長さが出ていないので、定まっているものの中から考えなければなりません。
三角形ADCは平行四辺形ABEDの半分の面積になります。したがってア+オは平行四辺形ABEDの半分です。
一方アとウも平行四辺形ABEDの半分になります。
よってア+オ=ア+ウですから、ウとオの面積が等しくなります。
(答え)ウとオ
(2)ア+ウ=イ イ=エ+8 ウ=オ ア=32 ア+イ+ウ+エ+オ=280cm2です。
ウ=【1】とするとオ=【1】 ア+オ=イなのでイ=32+【1】 エ=32+【1】-8=24+【1】から全体は
32+32+【1】+【1】+24+【1】+【1】=【4】+88=280から【1】=(280-88)÷4=48cm2
エ+オ=48+24+48=120cm2から120×2÷16=15cm
(答え)15cm
=============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
ある程度は切り捨てる
==============================================================
今日の慶應義塾進学情報
きれいに解く必要はない
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村

