2012 武蔵中学の図形の問題です。
次の図の長方形ABCDはたてが8㎝、よこが10㎝で、3つの長方形AEKH、IFCG、IJKLはどれもABCDを縮小した形です。
また、HLGDは正方形で、IJ=2㎝です。
次の問いに答えなさい。
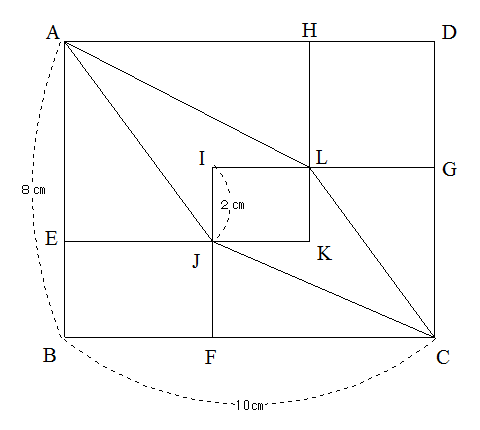
(1)HLの長さを求めなさい。
(2)四角形AJCLの面積を求めなさい。
いろいろ、解き方がある問題です。3つの長方形が相似形であることを利用していきましょう。
(1)
IJ:IL=4:5からIL=2.5㎝
正方形HLDGの一辺の長さを【1】として
8-【1】がGC 【1】+2.5がIGより
8-【1】:【1】+2.5=4:5から 内項の積=外項の積より
【4】+10=40-【5】 【9】=30より【1】=10/3
となります。
これは、長方形AEKHの適用してもよくて、
AH=10-【1】
AE=【1】+2
10ー【1】:【1】+2=5:4より内項の積=外項の積から
【5】+10=40ー【4】より【9】=30 【1】=10/3
と求めることができます。
(2)
せっかくIJKLが4:5の長方形だとわかっているので、これを使います。
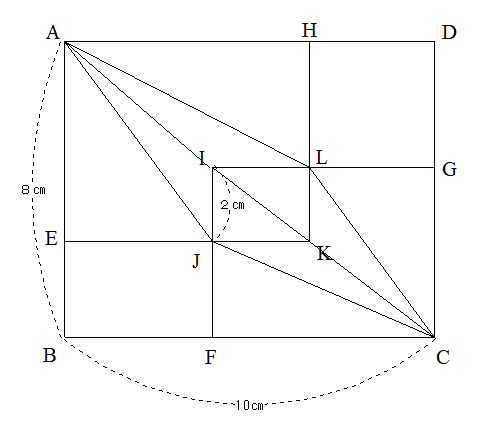
3つの長方形は相似形なのでAIKCは一直線上に並びます。
そうすると四角形AJCLは三角形AJCと三角形ALCに分けることができ、
三角形AJCは2×10÷2=10
三角形ALCも2×10÷2=10
したがって合計は10×2=20㎝2と計算することができます。
力づくでも答えは出ていくので、それで解いていった受験生もいると思いますが、条件をよく読んで使っていない条件がないか、考えてみることが必要です。
==============================================================
田中貴.com通信を発刊しています。登録は以下のページからお願いします。
無料です。
田中貴.com通信ページ
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
親の言うことを聞かない子
==============================================================
中学受験 算数オンライン塾
4月9日の問題
==============================================================
 「映像教材、これでわかる比と速さ」(田中貴) |
 6年算数重要問題精選ノート(田中貴) |
 「映像教材、これでわかる比と図形」(田中貴) |
