2018年開成中学の問題です。
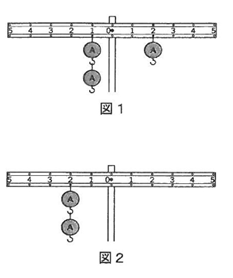
① 棒の真ん中を支点とした実験用てこがあります。図1のように,左のうでにおもりAを2個,右のうでにおもりAを1個下げると,棒は水平につり合います。棒の目盛りは等間隔とし,おもりA1個の重さを10gとして,以下の問いに答えなさい。
図2のように,左のうでにおもりAを2個下げました。図2の右のうでの目盛り1~5の5か所のうちの,どこか1か所だけにおもりAを何個か下げて,棒を水平につり合わせることを考えます。
問1 図2の右のうでのどこかにおもりAを1個下げると,棒は水平につり合いました。このとき,おもりAを下げた位置はどこですか。図2の右のうでの目盛り1~5の中から1つ選び,数字で答えなさい。
問2 図2の状態にもどした後,右のうでの目盛り1におもりAを何個か下げると,棒は水平につり合いました。このとき,右のうでに下げたおもり全部の重さは何9ですか。
問3 もう一度,図2の状態にもどした後,右のうでのどこか1か所だけにおもりを下げて,棒が水平につり合うときを考えます。このとき「支点から右のおもりまでの距離」と「右のおもり全部の重さ」は,比例の関係ですか,反比例の関係ですか。
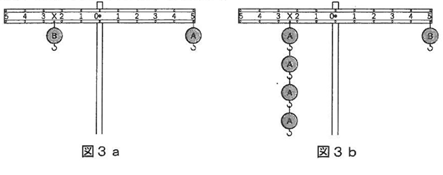
次に,棒の左のうでの,ある位置に目盛りXをとり,おもりを下げるための小さな穴をあけました。おもりAとは別のおもりBを用意して,図3aのように,左のうでの目盛り×におもりBを1個,右のうでの目盛り5におもりAを1個下げると,棒は水平につり合いました。また,図3bのように,左のうでの目盛りXにおもりAを4個,右のうでの目盛り5におもりBを1個下げても,棒は水平につり合いました。(図3aと図3bの目盛りXの位置は,正しく書かれてはいません。)
問4 図3aと図3bで,「支点から左右のおもりまでの距離の比」を,「片側のおもり全部の重さと,もう片側のおもり全部の重さの比」で表すと,どうなりますか。次の式の空らん,( あ )( い )に入るおもりの重さを答えなさい。
図3aの式
支点から目盛り×までの距離:5目盛り分の長さ=( あ )g : おもりB1個の重さ
図3bの式
支点から日盛り×までの距離:5目盛り分の長さ=おもりB1個の重さ:( い )g
問5 おもりB1個の重さは何9ですか。また,支点から目盛りXまでの距離は1日盛り分の長さの何倍ですか。割り切れない場合は,四捨五入して小数第1位まで求めなさい。
最後にもう一度,前のページの図2の状態にもどします。今度は,図2の右のうでの目盛り1~5の5か所のうちの何か所かにおもりAを何個か下げて,棒を水平につり合わせることを考えます。
問6 図2の右のうでのどこか2か所におもりAを1個ずつ下げると,棒は水平につり合いました。このとき,おもりAを下げた位置はどことどこですか。図2の右のうでの目盛り1~5の中から2つ選び,数字で答えなさい。
問7 図2の右のうでにおもりAを下げて,棒を水平につり合わせるやり方には,おもりを1か所に下げるやり方と,2か所に下げるやり方があります。図2の右のうでにおもりAを下げて,棒を水平につり合わせるやり方は,問1,問2,問6の場合をふくめて,全部で何通りありますか。
【解説と解答】
問1 2個が2の位置にあるので2×2÷1=4
(答え)4
問2 20×2÷1=40g
(答え)40
問3 積が一定ですから、反比例。
(答え)反比例
問4 支点からXまでの距離を(1)とし、Bの重さを<1>とすると、
(1)×<1>=10×5
(1)×40=<1>×5ですからあは10、いは40
(答え)あ 10 い 40
問5 10:B=B;40からB×B=400 B=20 20×5÷40=2.5
(答え)重さ 20 距離 2.5
問6 10×2=20 20×2=40だから10×1+10×3
(答え)13
問7 おもりを1ヶ所に下げる場合は20×2=40だから、1に40g 2に20g 4に10gの3通り
おもりを2ヶ所に下げる場合は10×1+10×3と 20×1+10×2の2通り 合計は5通り
(答え)5通り
Newオンライン中学入試説明会「これからの中学受験」のお知らせ
フリーダム進学教室 新連載 学校訪問シリーズ
New第7回 浦和明の星
受験で子どもと普通に幸せになる方法、本日の記事は
毎日のペースを作る
6年生の教室から
秋に向けて
中学受験 算数オンライン塾
9月1日の問題