2015年市川中学の問題です。
分数が並んでいる列に対して、次の操作を繰り返し行います。
操作:となりあう分数の分子にかかれている数字どうし、分母にかかれている数字どうしをたして新しい分数をつくり、これを2つの分数に間に入れる。ただし、約分はしないものとする。
最初に与えられた分数が$$\frac{1}{6}$$と$$\frac{3}{4}$$のとき
$$\frac{1}{6}$$、$$\frac{3}{4}$$
↓
操作1回目
↓
$$\frac{1}{6}$$、$$\frac{4}{10}$$、$$\frac{3}{4}$$
↓
操作2回目
↓
$$\frac{1}{6}$$、$$\frac{5}{16}$$、$$\frac{4}{10}$$、$$\frac{7}{14}$$、$$\frac{3}{4}$$
となります。
最初に与えられた分数の列が$$\frac{1}{2}$$、$$\frac{1}{3}$$のとき、次の問いに答えなさい。
(1)操作を4回行ったとき、右から7番目の分数を答えなさい。
(2)操作を7回行ったとき、並んでいる分数の数を答えなさい。
(3)操作を8回行ったとき、並んでいる分数んも分母の書かれている数字を全部加えるといくつになるか答えなさい。
(1)
操作1回目で3つ、このとき間の数は2個あるので、次は3+2=5個です。
操作2回目で5つです。このとき間の数は4個あるので、次は9個です。
操作3回目は9つです。
操作4回目は17です。
右から7番目です。このとき真ん中は右から9番目ですから、操作3回目の時に真ん中の数の右にできた数です。
したがって
$$\frac{2}{5}$$、$$\frac{3}{8}$$、$$\frac{1}{3}$$
$$\frac{2}{5}$$、$$\frac{5}{13}$$、$$\frac{3}{8}$$、$$\frac{4}{11}$$、$$\frac{1}{3}$$
となるから$$\frac{5}{13}$$です。
(答え)$$\frac{5}{13}$$
(2)
4回目は17個、5回目は17+16=33個 6回目は33+32=65個 7回目は65+64=129個です。
(答え)129個
(3)最初の分母の和は5、分子は2です。
1回目の結果を見ると、真ん中の数の2倍になっていることがわかります。
2回目の結果は真ん中の数の5倍です。
3回目は14倍です。
これを一覧にすると以下のようになります。

1回目は2と3が1回増えたので2倍になります。
2回目は2倍のところに3倍ふえたので5倍です。
3回目は5倍のところに9倍ふえたので14倍です。
4回目は14倍のところに27倍ふえたので41倍です。
前回新しく増えた数の3倍ずつ増えていくのでこのような規則になります。したがってこれを表にまとめると、
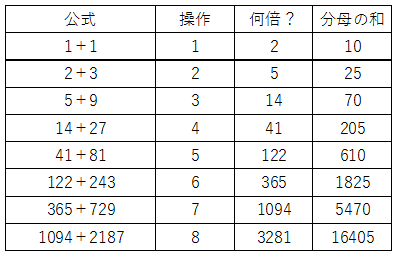
になるので、合計は16405です
(答え)16405
==========================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
プリントばっかり?
=============================================================
中学受験 算数オンライン塾
10月13日の問題
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村

