2016年ラ・サール中学の問題です。
AB=12cmの長方形ABCDがあります。図のように辺BC、CD上にそれぞれ点E、Fがあり、BE:EC=2:3、CF:FD=1:1です。このとき次の問に答えなさい。
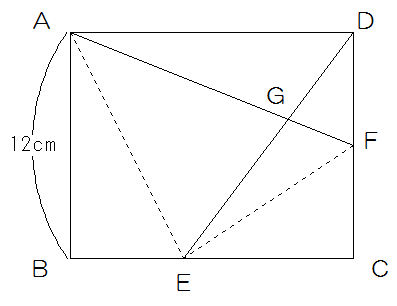
(1)三角形AEDと三角形DEFの面積比を最も簡単な整数比で求めなさい。
(2)三角形AEGの面積が60cm2のとき、三角形AEFの面積は何cm2ですか。
(3)(2)のとき、辺ADは何cmですか。
【解説と解答】
(1)三角形AEDは長方形の半分で、三角形DEFは長方形の$$\frac{3}{5}$$の半分の半分だから、10:3
(答え)10:3
(2)
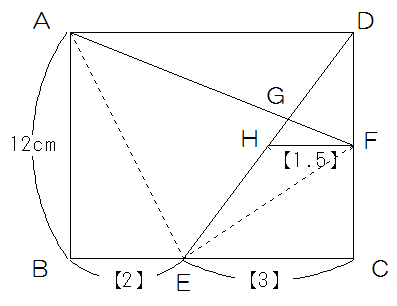
FからBCに平行に線を引きEDとの交点をHとすると、
EC=【3】HF=【1.5】 AD=【5】よりAG:GF=5:1.5=10:3
三角形AEG=60cm2より三角形AEF=60÷10×13=78
(答え)78cm2
(3)
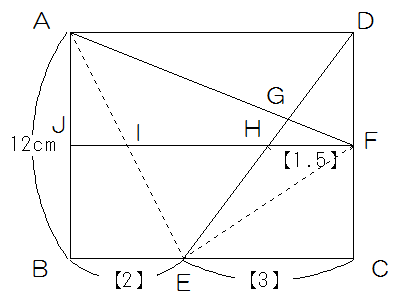
HFを延長してAEとの交点をI、AB十の交点をJとするとJI=【1】、IH=【5】-【1】-【1.5】=【2.5】
IF=【4】となります。
78×2÷12=156÷12=13cmがIFだから13÷4×5=16$$\frac{1}{4}$$
(答え)16$$\frac{1}{4}$$cm
「映像教材、これでわかる比と図形」(田中貴)
============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
ついていけない、と感じたら
=============================================================
中学受験 算数オンライン塾
3月15日の問題
==============================================================

==============================================================

==============================================================

==============================================================
![]()
にほんブログ村

