2014年早稲田実業の問題です。
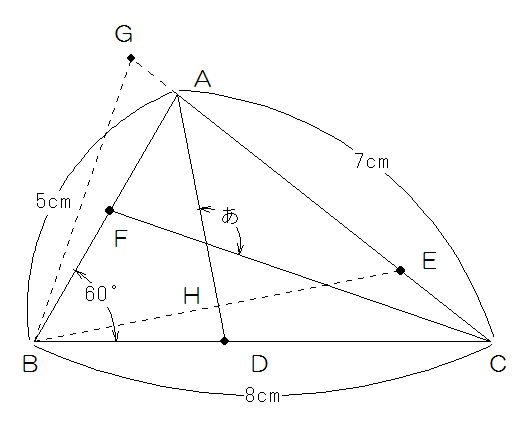
下の図のような角Bが60°の三角形ABCがあります。ADを折り目として三角形ABDを折り返したとき、頂点Bが辺AC上の点Eにきました。また、CFを折り目として三角形CBFを折り返したとき、頂点Bが辺CAを延ばした直線上の点Gにきました。次の問いに答えなさい。
(1)あの角度を求めなさい。
(2)ADとBEの交点をHとしたとき、三角形ABHの面積は三角形ABGの面積の何倍ですか。
【解説と解答】
(1)線分ADは角BACの二等分線になり、線分CFは角ACBの二等分線になります。
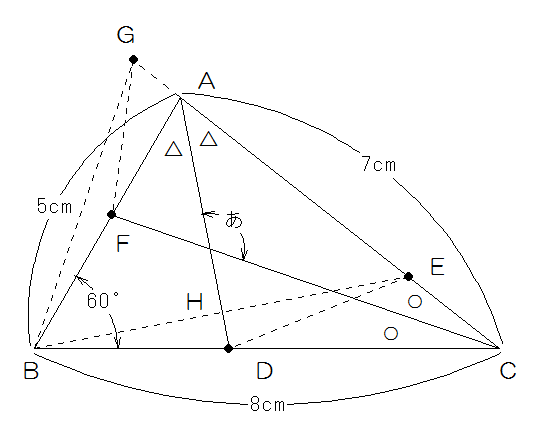
角BADを△、角ACFを○とすると、○○△△+60°が三角形ABCの内角の和になるので、
○○△△=180-60=120° ○△=120÷2=60°ですから、あは180-60=120°になります。
(答え)120°
(2)GC=8㎝、GA=1cmですから、三角形ABGは三角形ABCの$$\frac{1}{7}$$になります。
一方AE=5cmですから、三角形ABHは三角形ABCの$$\frac{5}{7}$$×$$\frac{1}{2}$$=$$\frac{5}{14}$$になります。
したがって$$\frac{5}{14}$$÷$$\frac{1}{7}$$=2.5倍です。
(答え)2.5倍
「映像教材、これでわかる比と図形」(田中貴)
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
夏休みは天王山ではない
==============================================================
今日の慶應義塾進学情報
正六角形の問題
==============================================================

==============================================================

==============================================================
![]()
にほんブログ村

