2017年麻布中学の問題です。
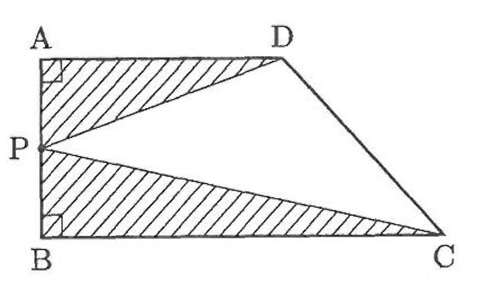
角Aと角Bが直角である台形ABCDがあり、ADの長さは6cm、BCの長さは10cm、面積は48cm2です.点Pが辺AB上にあるとして、三角形PADと三角形PBCの面積の和を考えます。次の( ア )から( ウ )に入る数を答えなさい。
(1)BPの長さが( ア )cmのとき、2つの三角形の面積の和は21cm2です。
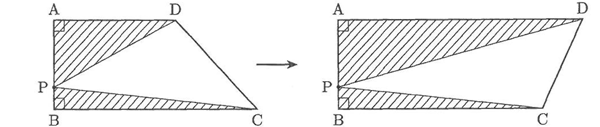
(2)BPの長さが( イ )cmのとき、下図のように点Dを動かしてADの長さをもとの2倍にのばすと、2つの三角形の面積の和はもとの$$\frac{10}{7}$$倍になります。
(3)BPの長さが( ウ )cmのとき、点Dを動かしてADの長さをもとの5倍にのばし、点Cを動かしてBCの長さをもとの2倍にのばすと、2つの三角形の面積の和はもとの$$\frac{10}{3}$$倍になります。
【解説と解答】
(1)AB=48×2÷(10+6)=6cmです。PB=6cmだと斜線部分の面積は6×10÷2=30cm2です。
1cm減ると6×1÷2+10×5÷2=3+25=28cm2と2cm2減るので、(30-21)÷2=4.5cm
6-4.5=1.5cm
(答え)1.5cm
(2)ADの長さが2倍になったので、12cmになりました。
三角形ABDの面積が2倍になったので、三角形ABD=【1】、三角形PBC=(1)とすると
【1】+(1):【2】+(1)=7:10 【14】+(7)=【10】+(10)より【4】=(3)になるから、
三角形APD:三角形PBC=3:4 AP:PB=$$\frac{3}{6}$$:$$\frac{4}{10}$$=5:4
6÷(5+4)×4=2 $$\frac{2}{3}$$
(答え)2 $$\frac{2}{3}$$cm
(3)ADの長さが6×5=30cm BCの長さが20cmです。
三角形ABDの面積が5倍、三角形PBCの面積が2倍になったので、三角形ABD=【1】、三角形PBC=(1)とすると
【1】+(1):【5】+(2)=3:10 【15】+(6)=【10】+(10)
【5】=(4)より
三角形APD:三角形PBC=4:5 AP:PB=$$\frac{4}{6}$$:$$\frac{5}{10}$$=4:3
6÷(4+3)×3=2 $$\frac{4}{7}$$
(答え)2 $$\frac{4}{7}$$cm
=============================================================
5月27日 ”追加”中学入試説明会 「学校別対策の考え方」のお知らせ
=============================================================
受験で子どもと普通に幸せになる方法、本日の記事は
本人なりの努力
6年生の教室から
自分でやりたいから反抗する
今日の慶應義塾進学情報
南西諸島に関する問題