2017年駒場東邦の問題です。
次のように、分子が1以上434以下の整数で、分母が435である分数を小さい順にならべたものを考えます。
$$\frac{1}{435}$$、$$\frac{2}{435}$$、$$\frac{3}{435}$$、・・・$$\frac{434}{435}$$
(1)それ以上約分できない分数のことを既約分数と言います。次の分数を既約分数で表しなさい。
1)$$\frac{285}{435}$$
2)$$\frac{377}{435}$$
(2)既約分数は全部でいくつあるか答えなさい。
(3)既約分数ではない分数がもっとも長く続く並びをすべて求めなさい。ただし約分はせず$$\frac{A}{435}$$~$$\frac{B}{435}$$のように答えなさい。
【解説と解答】
(1)
1)285=5×57=3×5×19 435=5×87=3×5×29
より$$\frac{19}{29}$$
2)377=13×29より
$$\frac{13}{15}$$
(2)
既約分数は1から434の中で3でも5でも29でも割れない数、ということになります。
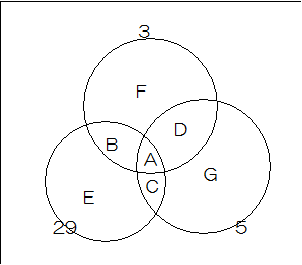
A=0、B=4 C=2 D=28 F=144-32=112 G=86-30=56 E=14-6=8
4+2+28+112+56+8=210
434-210=224
(答え)224個
(3)
3と5と29の倍数が続くところです。29の倍数で3と5の倍数ではないものを考えていくと
29×1=29、30まで。
29×2=58より57、58まで。
29×4=116から114、115、116、117と4つ続きます。
29×7=203より203、204、205、は該当しません。
29×8=232から230、231、232、は該当しません。
29×11=319より318、319、320、321と4つ続きます。
29×13=377より377、378まで。
より
114から117と318~321
(答え)114から117と318~321
受験で子どもと普通に幸せになる方法、本日の記事は
面倒見の良い塾?
5年生の教室から
清書のすすめ
中学受験 算数オンライン塾
2月14日の問題




