2016年東大寺学園の問題です。
円柱の形をした鉄のかたまりア、イ、ウがあります。ア、イ、ウの底面積はそれぞれ100 cm2、150 cm2、300 cm2でア、イ、ウの高さの合計は95cm です。
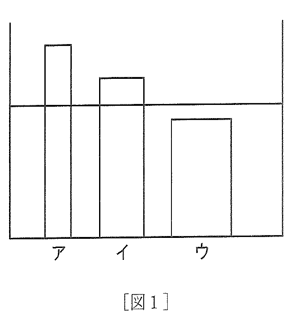
(1)[図1]のように水の入っている水そうにア、イ、ウをまっすぐに立てます。
このとき、アの高さの$$\frac{2}{5}$$、イの高さの$$\frac{1}{4}$$でが水面から出ていました。
また、ウの上の面は水面よりlcm下のところにありました。
①アとイの高さの比を求めなさい。
②ウの高さを求めなさい。
(2)[図1]の状態からアを水そうから取り出すと、ウの上の面は水面より1cmのところにありました。水そうの底面積を求めなさい。
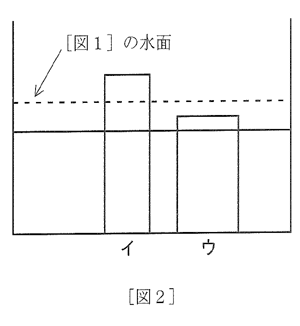
(3)[図2]の状態からイとウを取り出したときの水面の高さを求めなさい。
【解説と解答】
(1)
[図1]の水面の高さを【3】とすると、アの高さは【5】、イの高さは【4】、ウの高さは【3】-1 になります。
① ア:イ=5:4です。
(答え)5:4
② 合計が95cmですから、【12】-1=95 【1】=8cmになるので、8×3-1=23cmになります。
(答え)23cm
(2)水の体積は変わっていません。
最初の高さは24cmでしたから、水槽の底面積を<1>cm2とすると(<1>-550)×23+(<1>-250)×1=<23>-12650+<1>-250=<24>-12900が水の体積です。
一方アを抜いたあと水面は23-1=22cmですから、(<1>-450)×22=<22>-9900=<24>-12900
より<2>=3000 <1>=1500cm2
(答え)1500cm2
(3)水の容積は1500×22-9900=23100cm3ですから、23100÷1500=15.4
(答え)15.4cm
============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
暗記テキストの盲点
============================================================
中学受験 算数オンライン塾
6月21日の問題
==============================================================

==============================================================

==============================================================

==============================================================
![]()
にほんブログ村
0620