2015年栄光学園の問題です。
3つの水そうア、イ、ウと3つの注水口A、B、Cがあります。アとウの容積は同じで、イの容積はアの半分です。注水口A、B、Cから出る1分あたりの水の量はそれぞれ一定です。Aだけで水そうアに水を入れると20分でいっぱいになり、Bだけで水そうアに水を入れると15分でいっぱいになります。
(1)図1のようにA、Bから空の水そうアに同時に水を入れはじめると、何分でいっぱいになるか答えなさい。
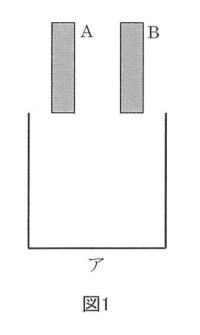
注水口の先につなぐことのできる3つの装置X、Y、Zがあります。これらは、それぞれ一定の割合で水を分けることができます。
(2)図2のようにA、Bから空の水そうア、イに同時に水を入れはじめると、アとイはちょうど同じ時間でいっぱいになりました。このとき、かかった時間を答えなさい。また、装置Ⅹによって、Bからアとイに分けられた水の量の比を答えなさい。
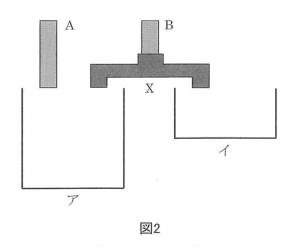
(3)図3のように、装置Y、Zをつなぎます。装置ZはCの水をイとウに1:3の割合で分けます。A、B、Cから空の水そうア、イ、ウに同時に水を入れはじめると、ア、イ、ウはちょうど同じ時間でいっぱいになりました。このとき、装置YによってBからアとイに分けられた水の量の比を答えなさい。
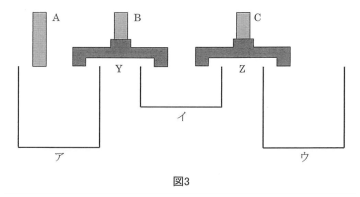
【解説と解答6
(1)
アの容積を【60】とするとイの容積は【30】Aは1分に【3】、Bは1分に【4】入れることができることがわかります。
したがって60÷7=8$$\frac{4}{7}$$分
(答え)8 $$\frac{4}{7}$$分
(2)
アとイの合計は【90】で、AとBの1分あたりの和は【7】ですから、満水になるまでの時間は90÷7=$$\frac{90}{7}$$分=12 $$\frac{6}{7}$$分です。
Aはその時間で【3】×$$\frac{90}{7}$$=【$$\frac{270}{7}$$】 【60】ー【$$\frac{270}{7}$$】=【$$\frac{150}{7}$$】
【$$\frac{150}{7}$$】:【30】=5:7です。
(答え)12 $$\frac{6}{7}$$分 5:7
(3)
満水になった時間が同時になので、アに入った水とイに入った水とウに入った水の比は2:1:2です。
Aからアに入った水は1分あたり【3】、Bからアに入った水を1分当たりP、Bからイに入った水を1分当たりQ、Cからイに入った水を1分あたり(1)、Cからウに入った水を1分あたり(3)とすると、
Q+(1)=(3)÷(2)=(1.5)
Q=(0.5)
【3】+P=(3)
P+Q=【4】
Q=(0.5)ですから、P=【4】-(0.5) 【4】-(0.5)+【3】=(3)より【7】=(3.5)(1)=【2】です。
したがってP=(1.5)ですから、P:Q=1.5:0.5=3:1になります。
(答え)3:1
==============================================================
中学受験で子どもと普通に幸せになる方法、本日の記事は
しっかり勉強しなさい、ただし疲れてはいけない
==============================================================
今日の慶應義塾進学情報
先のことはわからない
==============================================================

==============================================================
==============================================================

==============================================================
![]()
にほんブログ村
